HOW CAN ultraviolet disinfection lamp (UVC) KILL bacteria
WHAT IS THE ULTRAVIOLET LAMP?
Ultraviolet (UVA light /UVB light /UVC light ) lamp is a short wavelength lamp range from 100nm to 400nm,the uvc is 100-280nm ,which can kill bacteria (the best uv light kills bacteria).and uvb (365nm) & uva(395nm).
Ultraviolet sterilization and disinfection has already become a widely used by mature technology. The emergence of the new coronavirus pneumonia epidemic has aroused renewed attention and interest and some ultraviolet sterilization lamp and disinfection equipment has become hot.
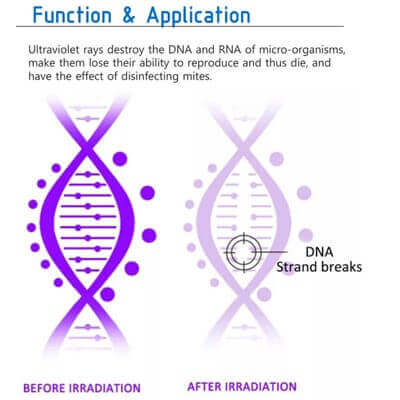
It is an indisputable fact that ultraviolet radiation can effectively kill bacteria and viruses. In the theory, the new coronavirus can also be effectively killed by a sufficient amount of ultraviolet radiation. However, only by properly grasping the relevant knowledge of ultraviolet sterilization and disinfection technology, especially the effective control of the dosage of ultraviolet sterilization and disinfection, can the relevant tools and equipment be used in a standardized manner to obtain the ideal disinfection and disinfection effect.
The energy of an optical radiation particle is inversely proportional to the wavelength, so ultraviolet radiation in the short wavelength band of the optical radiation spectrum has a higher energy of a single particle, and they can destroy the deoxyribonucleic acid (DNA) in the bacterial virus when irradiated on the bacterial virus.
HOW CAN ULTRAVIOLET LIGHT KILL GERMS?The molecular structure of ribonucleic acid (RNA) causes the rupture of the DNA chain and the cross-linking of nucleic acid and protein, leading to the growth and death of regenerative cells, which achieves the effect of sterilization and disinfection. Experiments show that ultraviolet radiation with a wavelength of 205-305 nm has a certain sterilization effect, especially the effect of 240-280 nm ultraviolet radiation is particularly significant. Low-pressure mercury lamp, commonly known as ultraviolet sterilization lamp, is currently the most widely used ultraviolet radiation source for sterilization and disinfection. (uv light disinfection/sterilization)
Its radiation is mainly concentrated in the spectral line with a wavelength of 253.7 nm, which is located in the band with the most significant ultraviolet radiation sterilization and disinfection effect. Therefore, it is the most efficient source of ultraviolet sterilization and disinfection radiation.
The effect of ultraviolet sterilization and disinfection is determined by the ultraviolet radiation dose to the microorganisms: the greater the radiation dose, the higher the sterilization and disinfection efficiency. The ultraviolet radiation dose is the ultraviolet radiation energy received per unit area and is the integral of ultraviolet irradiance to time. When the intensity of the radiation source is substantially unchanged, the ultraviolet radiation dose is equal to the product of ultraviolet irradiance and irradiation time.
In fact, the dose of ultraviolet radiation required to kill different bacterial viruses is different. Experiments have shown that if a low-pressure mercury lamp is used as a radiation source, the ultraviolet radiation dose to kill carbon maggots or Tetanus bacillus is 9 mJ / cm2, and the ultraviolet radiation dose to kill E. coli or Mycobacterium tuberculosis is 12 mJ / cm2. The ultraviolet radiation dose of dysentery bacillus was 45 mJ / cm2; the ultraviolet radiation dose to kill influenza virus was 9 mJ / cm2, and the ultraviolet radiation dose to kill hepatitis B virus was 24 mJ / cm2. Although there is no accurate ultraviolet radiation dose to effectively kill the new coronavirus, relevant experiments have shown that the ultraviolet radiation dose to effectively kill the SARS virus does not exceed 300 mJ / cm2.
Therefore, using a 100 mJ / cm2 ultraviolet radiation dose can kill most bacteria and viruses, which is equivalent to an ultraviolet irradiance of 5 mW / cm2 (close to the low-pressure mercury lamp wall available irradiance) irradiation target 20 s or ultraviolet irradiance 80 μW / cm2 (irradiance obtained at 1 m below the 30 W low-pressure mercury lamp) irradiation target for 20 min.
The key to controlling the ultraviolet radiation dose is the determination of the ultraviolet irradiance at the irradiation target, which is usually measured with an ultraviolet irradiator. It should be noted that the ultraviolet radiation source often needs to be powered on for a few minutes to achieve a stable radiation output, so the measurement must also be performed a few minutes after the radiation source is powered on.
Bacteria and viruses can be killed within a few seconds under strong ultraviolet radiation, so fast, universal, low heat and non-contact are the most prominent advantages of ultraviolet sterilization methods. For a long time, it has become one of the main means of disinfection of operating rooms, burn wards, infectious wards and sterile workshops in medical and health, food production and other fields, as well as disinfection of heat-resistant items and table surfaces. In recent years, because the ultraviolet sterilization and disinfection methods will not introduce impurities into the water and affect the water quality, and the emergence of short-wave ultraviolet LEDs, water treatment and home office air purification have become new hot spots in the application of ultraviolet sterilization and disinfection methods.
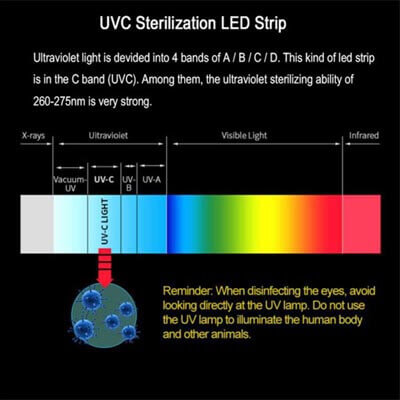
You can check some of germicidal lamp below:
Although the single particle energy of ultraviolet radEiation is high, its penetration is weak, and it can only kill the microorganisms directly irradiated. Therefore, it is only suitable for the killing of bacteria and viruses on the target surface. This is the main limitatioron of the ultraviolet sterilization method, so When using ultraviolet sterilization and disinfection methods, the sterilization and disinfection parts must be fully exposed to ultraviolet radiation. When used for sterilization and disinfection of solid surfaces such as fabrics and papers, both sides should be irradiated.
In daily life, many people put fabrics in the sun to dry to sterilize, because sunlight also contains a certain amount of ultraviolet radiation. However, due to the absorption of the atmospheric ozone layer, only solar radiation with a wavelength greater than 290 nm can penetrate the atmosphere and reach the ground, and its wavelength is shorter than 305 nm. The proportion of radiation that is shorter than 305 nm is very small. In the hot sun for a long time, it should also be noted that the warming caused by the rich infrared radiation in the sun also has a certain effect of killing bacteria and viruses.
It must be emphasized that when using ultraviolet sterilization and disinfection methods, you must attach great importance to your own safety protection, because short-wave ultraviolet radiation can also cause damage to the human body as an organism, mainly to avoid direct exposure of the skin, especially the human eye. Short-wave ultraviolet radiation, fabric shielding, wearing glasses, etc. are all effective protective means that can be used.
